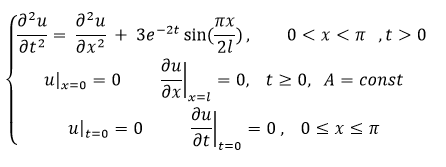Условие:
Решить смешанную задачу
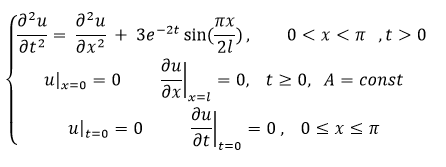
Решение:
Это задача по предмету "Математика", конкретно по разделу "Дифференциальные уравнения" или "Физика", в зависимости от контекста задачи. В данном случае мы имеем дело с волновым уравнением с граничными условиями. Рассмотрим данное волновое уравнение:
\[ \frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2} + 3e^{-2t} \sin\left(\frac{\pi x}{2l}\right), \]
\[ 0 < x < \pi, \; t > 0, \; A = const. \]
С граничными и начальными условиями:
\[ u|_{x=0} = 0, \; \frac{\partial u}{\partial x}\bigg|_{x=l} = 0, \; t \ge 0, \]
\[ u|_{t=0} = 0, \; \frac{\partial u}{\partial t}\bigg|_{t=0} = 0, \; 0 \le x \le \pi. \]
Мы будем решать эту задачу методом разделения переменных и преобразование Фурье.
Шаг 1: Решим однородную часть уравнения
Для однородной части уравнения без правой части:
\[ \frac{\partial^2 u}{\partial t^2} = \frac{\partial^2 u}{\partial x^2}, \]
предположим, что решение имеет вид
\( u(x,t) = X(x)T(t) \).
Разлагаем уравнение:
\[ X(x) \frac{d^2 T}{d t^2} = T(t) \frac{d^2 X}{d x^2}.\]
Разделяем переменные:
\[ \frac{1}{T}\frac{d^2 T}{d t^2} = \frac{1}{X}\frac{d^2 X}{d x^2} = -\lambda, \]
где
\(\lambda\) -- некоторая постоянная.
Шаг 2: Решим уравнения для
\(X(x)\)
и
\(T(t)\)
Для функции
\(X(x)\)
имеем:
\[ \frac{d^2 X}{d x^2} + \lambda X = 0. \]
Решим это уравнение с граничными условиями:
\[ X(0) = 0, \; \frac{dX}{dx}\bigg|_{x=l} = 0. \]
Общее решение имеет вид:
\[ X(x) = A \sin\left(\sqrt{\lambda} x\right) + B \cos\left(\sqrt{\lambda} x\right). \]
Из граничного условия
\(X(0) = 0\)
следует, что
\( B = 0 \).
Из условия
\(\frac{dX}{dx}\bigg|_{x=l} = 0\)
получаем:
\[ \sqrt{\lambda} A \cos\left(\sqrt{\lambda} l\right) = 0. \]
Поскольку
\( \sqrt{\lambda} \cos\left(\sqrt{\lambda} l\right) = 0,\)
то
\( \cos\left(\sqrt{\lambda} l\right) = 0.\)
Следовательно:
\[ \sqrt{\lambda} l = \left(n + \frac{1}{2}\right) \pi, \; n \in \mathbb{Z}. \]
Отсюда:
\[ \lambda = \left(\frac{(2n+1) \pi}{2l}\right)^2. \]
Подставим в уравнение для
\(T(t)\):
\[ \frac{d^2 T}{d t^2} + \left(\frac{(2n+1)\pi}{2l}\right)^2 T = 0. \]
Решение имеет вид:
\[ T(t) = C \cos\left(\frac{(2n+1)\pi t}{2l}\right) + D \sin\left(\frac{(2n+1)\pi t}{2l}\right).\]
Шаг 3: Соберем общее решение
Полное решение будет:
\[ u(x,t) = \sum_{n=0}^{\infty} \left[ C_n \cos\left(\frac{(2n+1)\pi t}{2l}\right) + D_n \sin\left(\frac{(2n+1)\pi t}{2l}\right) \right] \sin\left(\frac{(2n+1)\pi x}{2l}\right). \]
Шаг 4: Учитываем начальные условия
Используя начальные условия, определим коэффициенты
\(C_n\)
и
\(D_n\).
Начальное условие
\(u|_{t=0} = 0\):
\[ \sum_{n=0}^{\infty} C_n \sin\left(\frac{(2n+1)\pi x}{2l}\right) = 0. \]
Отсюда
\(C_n = 0.\)
Начальное условие
\(\frac{\partial u}{\partial t}\bigg|_{t=0} = 0\):
\[ \sum_{n=0}^{\infty} \frac{(2n+1) \pi}{2l} D_n \sin\left(\frac{(2n+1)\pi x}{2l}\right) = 0. \]
Отсюда следует
\(D_n = 0\).
Шаг 5: Правую часть добавим к решению
Поскольку начальные условия равны нулю, и
\(C_n\)
и
\(D_n\)
также равны нулю, ищем частное решение для неоднородной части:
\[ u_{part} (x,t). \]
Ищем в форме:
\[ u_{part} (x,t) = f(t) \sin\left(\frac{\pi x}{2l}\right). \]
Подстановка в уравнение:
\[ \sin\left(\frac{\pi x}{2l}\right) \frac{d^2 f}{d t^2} = \sin\left(\frac{\pi x}{2l}\right) \frac{\pi^2}{4l^2} f + 3e^{-2t} \sin\left(\frac{\pi x}{2l}\right). \]
Сократим
\(\sin\left(\frac{\pi x}{2l}\right)\):
\[ \frac{d^2 f}{d t^2} = \frac{\pi^2}{4l^2} f + 3e^{-2t}. \]
Ищем решение методом вариации постоянных. Пусть частное решение:
\[ f(t) = Ae^{-2t} + Be^{2t},\]
тогда
\[ \frac{d^2 f}{d t^2} = 4Ae^{-2t} + 4Be^{2t}. \]
Подставим в уравнение:
\[ 4Ae^{-2t} + 4Be^{2t} = \frac{\pi^2}{4l^2} (Ae^{-2t} + Be^{2t}) + 3e^{-2t}. \]
Решаем относительно постоянных:
\[ A = \frac{3}{4 - \frac{\pi^2}{4l^2}}, B = 0. \]
Таким образом, частное решение:
\[ f(t) = \frac{3}{4 - \frac{\pi^2}{4l^2}} e^{-2t}.\]
И общее решение:
\[ u(x,t) = \frac{3}{4 - \frac{\pi^2}{4l^2}} e^{-2t} \sin\left(\frac{\pi x}{2l}\right).\]
Ответ:
\[ u(x,t) = \frac{3}{4 - \frac{\pi^2}{4l^2}} e^{-2t} \sin\left(\frac{\pi x}{2l}\right).\]